Selection bias

class: center, middle, inverse, title-slide

# Selection bias
## What If: Chapter 8
### Elena Dudukina
### 2021-02-18

---

# Selection bias
## Classic definition
- The magnitude of the association is different for participants and non-participants
## Structural definition
- Occurs when conditioning on the common child or its descendants of two variables
## Encompasses various biases
---
# 8.1 The structure of selection bias
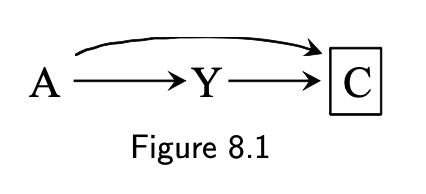
DAG:
- A: exposure (folic acid supplements)
- Y: outcome, binary (cardiac malformation)
- C: common effect (death before birth) observed only among live-born children (C=0)
![:scale 30%](Screenshot 2021-02-17 at 14.19.10.png)
---
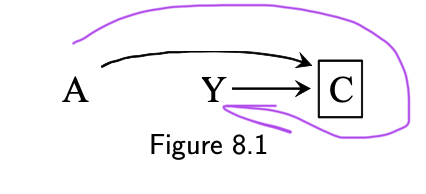
# Under the null
- The biasing path A ➡️ [C] ⬅️ Y

- The associational risk ratio **does not** equal causal risk ratio
    - `\(\frac{Pr[Y=1|A=1, C=0]}{Pr[Y=1|A=0, C=0]}\)` is not `\(\frac{Pr[Y^{a=1}]}{Pr[Y^{a=0}]}\)`
    
    
![:scale 30%](Screenshot 2021-02-17 at 17.44.36.png)
---
# Selection bias
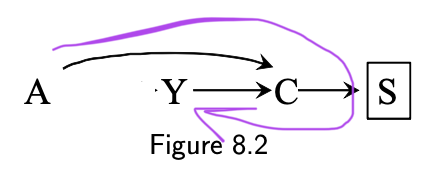
DAG:
- A: exposure (folic acid supplements)
- Y: outcome, binary (cardiac malformation)
- C: common effect (death before birth) observed only among live-born children (C=0)
- S: parental grief (restricted to S=0)

Under null we would still see an association between A and Y due to the collider stratification bias
  - The biasing path A ➡️ [C] ⬅️ Y

![:scale 30%](Screenshot 2021-02-17 at 17.51.30.png)
---
# Selection bias
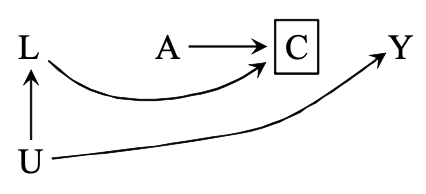
- DAG 8.3: 
    - A: anti-retroviral treatment
    - Y: 3-year risk of death
    - U: unmeasured, immunosuppression (U=1 are under greater risk of death)
    - C: censored (C=1)
    - L: unmeasured, immunosuppression symptoms
    
Biasing path:
- A ➡️ [C] ⬅️ L ⬅️ U ➡️ Y

![:scale 30%](Screenshot 2021-02-17 at 17.55.54.png)
---
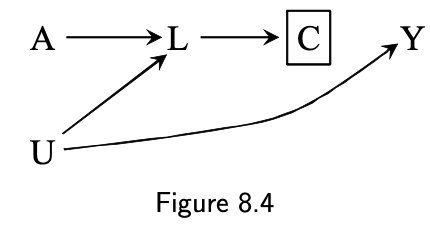
# Selection bias
- DAG 8.4: 
    - A: anti-retroviral treatment
    - Y: 3-year risk of death
    - U: unmeasured, immunosuppression (U=1 are under greater risk of death)
    - C: censored (C=1)
    - L: unmeasured, immunosuppression symptoms
    
Biasing path: 
- A ➡️ [L] ⬅️ U ➡️ Y

![:scale 30%](Screenshot 2021-02-17 at 18.05.56.png)

---
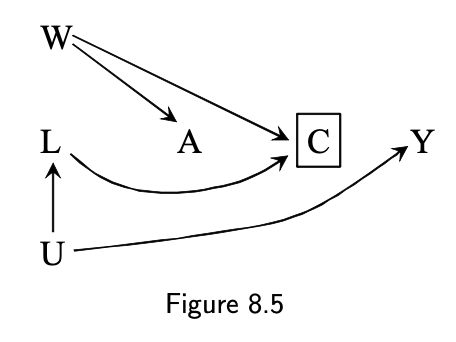
# Selection bias
- DAG 8.5 (M-bias): 
    - A: anti-retroviral treatment
    - Y: 3-year risk of death
    - U: unmeasured, immunosuppression (U=1 are under greater risk of death)
    - C: censored (C=1)
    - L: unmeasured, immunosuppression symptoms
    - W: unmeasured, lifestyle
    
![:scale 30%](Screenshot 2021-02-17 at 18.41.35.png)
---
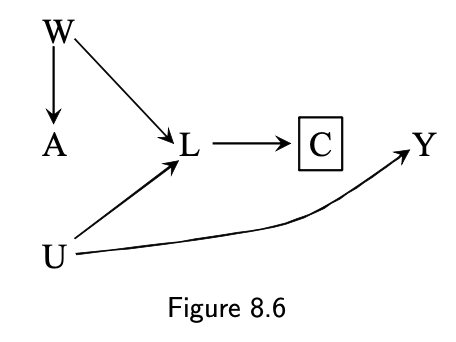
# Selection bias
- DAG 8.6 (M-bias): 
    - A: anti-retroviral treatment
    - Y: 3-year risk of death
    - U: unmeasured, immunosuppression (U=1 are under greater risk of death)
    - C: censored (C=1)
    - L: unmeasured, immunosuppression symptoms
    - W: unmeasured, lifestyle
    
![:scale 30%](Screenshot 2021-02-17 at 18.42.46.png)
---
# 8.2 Examples of selection bias
- Differential loss to follow-up/informative censoring (8.3-8.6)
- Missing data bias, non-response bias
    - Missing data on the outcome for any reason  (8.3-8.6)
- Healthy worker bias
    - U: unmeasured, underlying health
    - C: at work or not (C=0 being at  work)
- Self-selection bias, volunteer bias
- Selection affected by treatment received before study entry

Selection bias can occur in any follow-up study (observational or RCT)
- Those who stayed in the study (uncensored, C=0) are not exchangeable with those who did not stay in the study (censored, C=1)
    - Can only compute observational `\(\frac{Pr[Y=1|A=1, C=0]}{Pr[Y=1|A=0, C=0]}\)`, but not counterfactual `\(\frac{Pr[Y^{A=1, C=c}]}{Pr[Y^{A=0, C=c}]}\)` under both levels of C={0, 1}
---
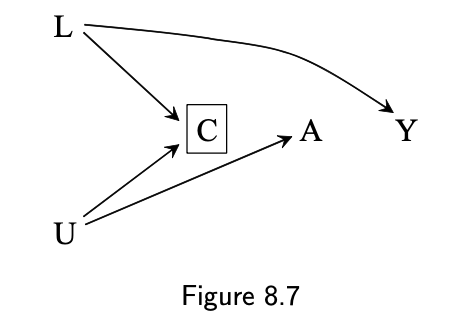
# 8.3 Selection bias and confounding
Sources of lack of exchangeability:
- Confounding
- Selection bias

DAG 8.7:
- A: physical activity
- Y: heart disease
- L: family SES
- C: becoming a firefighter (restricted to C=1)
- U: unmeasured, personal preference for physical activity professions

There is no confounding between A and Y
`\(\frac{Pr[Y=1|A=1, C=0]}{Pr[Y=1|A=0, C=0]}\)` is `\(\frac{Pr[Y^{a=1}]}{Pr[Y^{a=0}]}\)`

![:scale 25%](Screenshot 2021-02-17 at 19.01.19.png)
---
# 8.4 Selection bias and censoring
- Censoring as "treatment"
- Identifiability conditions of exchangeability, positivity, and consistency hold for both A and C
- Analytical methods

---
# 8.5 How to adjust for selection bias
- IP weighting (or standardization)
    - Assigning a weight to each selected individual (C = 0) that accounts for the individuals with same A and L, but C=1
    - Weights constructed from the probability of selection model: `\(Pr[C=0|L, A]\)`
- Effect measure in the population had no one been censored
---
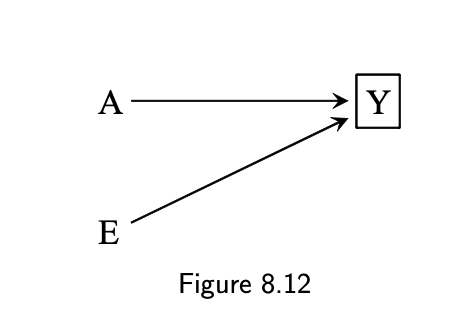
# 8.6 Selection without bias
- A: surgery
- Y: death
- E: haplotype

![:scale 30%](Screenshot 2021-02-17 at 19.35.24.png)
---
![:scale 30%](Screenshot 2021-02-17 at 19.39.32.png)
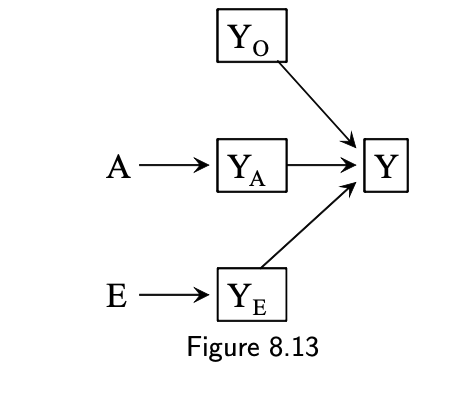
- "Collider stratification is not always a source of selection bias"
---
# References
Hernán MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC (v. 31jan21)